/// This article is extracted from Mårten Nettelbladt’s works. Have a look to his reasearch blogs, here and here ///
DEFINITION. Forms are called ‘developable’ or ‘single curved’ when they can be created through ordinary bending of a planar surface without stretching, cutting or wrinkling the material. These surfaces are characterized by only bending in one direction at a time, like the cylinder or the cone. Developable surfaces are useful because they allow round forms to be made out of flat materials like plywood, sheet metal or cloth. This is why they are used for ship building, tent sewing and fabrication of ventilation ducts etc.

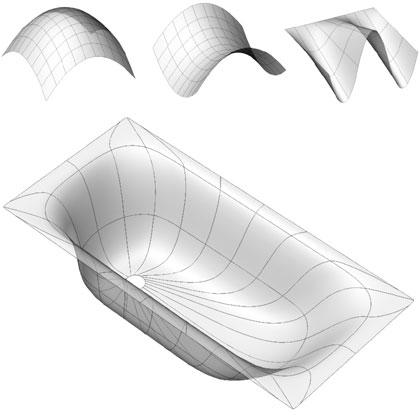
DOUBLE CURVED. Surfaces that bend in two directions at the same time and cannot be made out of a flat material are called ‘double curved’. The sphere and the saddle are examples of such surfaces (no double curved surfaces are developable). ‘Ruled surfaces’ are constructed from straight lines and are either developable or double curved. Because they appear to be straight in one ‘direction’ they can be mistaken for developable surfaces when they are in fact double curved.
TYPES. four types of developable surfaces:
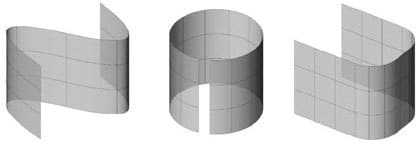
1. Cylindrically developable. A curve extruded straight, creating a surface with a constant section. If the curve is a circle, the surface will be a cylinder.
2. Conically developable. A curve extruded towards a focal point results in a surface with a section varying in size. A circle shaped curve produces a cone.

3. Poly-conically developable. Surfaces of the two first categories joined together create a composite surface consisting of conical (and cylindrical) segments.
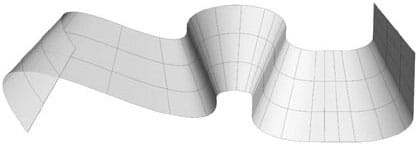
4. Super-poly-conically developable. If a poly-conic surface (type 3) changes focal point momentarily, the resulting surface curves in a smoother way and can no longer be divided into segments.

from: https://www.omkrets.se/

https://thegeometryofbending.blogspot.com/ (I’m looking at the type of bending that is elastic (not plastic), meaning the material will spring back to its original shape when the force is released. Most materials break or deform permanently before they can reach an ‘elastic and beautiful curve’, but I think all ‘elastic deformation’ follow the same principals and therefore the same geometry.
/// This article is extracted from Mårten Nettelbladt’s works. Have a look to his reasearch blogs, here and here ///
developable surfaces
4,6K
previous post

2 comments
ahahahah!
simple
cool
et utile!
[…] have already talked about Mårten Nettelbladt as a very interesting researcher on topics of complex geometries, and specifically the topic of […]